这里给出一种非现实的计算模型：非确定图灵机。顾名思义，它的移动不能被转移函数唯一确定，即，非确定图灵机的转移函数是一个多值函数。另外以指数效率为代价，非确定图灵机可以被确定图灵机模拟，这也符合Church-Turing 命题，即所有合理的计算模型可以互相模拟。然而，该指数代价是问题固有的还是由于我们理解的局限性造成的，目前还没有明确的答案，此即为著名的问题$P$等不等于$NP$，如果能把确定图灵机模拟非确定图灵机的代价降到多项式，$P$就等于$NP$，否则就不等。

    一个非确定图灵机是一个四元组$N=(K,\Sigma,\Delta,s)$，其中$K,\Sigma,s$和确定图灵机是一样的，但转移函数$\Delta$发生了改变，它的每次转移得到的结果不是唯一确定的，而是在一组结果里面随机选择一个。因此，$\Delta$不再是$K\times \Sigma$到$(K\cup \{h,yes,no\})\times \Sigma\times \{\rightarrow,\leftarrow,-\}$的映射，而是：

$$\Delta \subseteq (K\times \Sigma)\times[(K\cup \{h,yes,no\})\times \Sigma\times \{\rightarrow,\leftarrow,-\}]$$

即$\Delta$是一个关系，对于每个状态符号组合$(q,\sigma)$，或存在不止一个下一步转移的合适选择或者没有下一步转移。另外，对每个$(q,\sigma) \in K\times \Sigma$，定义集合$C_{(q,\sigma)}=\{(p,\rho,D):((q,\sigma),(p,\rho,D))\in \Delta\}$，则此集合里包含$(q,\sigma)$所有可能的转移，令$d=\underset{(q,\sigma)}{max}|C_{(q,\sigma)}|$，则称$d$为非确定图灵机$N$的非确定度。

    非确定图灵机的运行实际上是一个树形结构，如下图所示，每个瞬时像都对应着多个可能的转移，依次进行，最终进入停机状态。

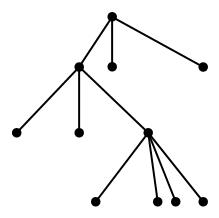
非确定图灵机的转移路径非常多，其总和是指数级别的，只要有一条路径进入$yes$状态，就可以认为此图灵机输出$yes$，。若没有任何一条转移路径使得机器进入$yes$状态，则认为此图灵机输出$no$，这里是默认图灵机$N$最终肯定会停机，所以要么有$yes$状态，要么都不是$yes$状态。

    如果$N$判定语言$L$，而且对于任意输入$x\in\Sigma^*$，转移函数的转移次数$k\leq f(|x|)$(即$N$的计算活动的最长路径为$f(|x|)$)，则称非确定图灵机$N$在时间$f(n)$内判定语言$L$。由此类似于确定图灵机，可以直接定义带有输入-输出带的多带非确定图灵机。定义复杂类$NTIME(f(n))$为在时间$f(n)$内由非确定图灵机判定的语言类的集合。同时类似于确定性图灵机，对于非确定图灵机有线性加速定理：

对于任意$\epsilon>0$，$NTIME(f(n))=NTIME(\epsilon f(n)+n+2)$

于是，对于任意$k$次多项式$f(n)$，有$NTIME(f(n))=NTIME(n^k)$，则可定义复杂类

$$NP=\underset{k\geq 0}{\cup}NTIME(n^K)$$

显然$P\subseteq NP$

    非确定图灵机的空间和确定图灵机是类似的，若对于任意输入$x$，$N$停机所需要空间至多为$f(|x|)$，则称非确定图灵机$N$在空间界$f(n)$内运行。给定一个带有输入输出带的$k$带非确定图灵机$N=(K,\Sigma,\Delta,s)$，称在空间$f(n)$内$N$判定语言$L$，如果$N$判定$L$所需要的空间至多为$f(|x|)$。令$NSPACE(f(n))$为带有输入输出带的非确定图灵机$N$在空间$f(n)$内判定的语言类，则对于非确定图灵机有下列空间压缩定理。

对于任意$\epsilon>0$，$NSPACE(f(n))=NSPACE(\epsilon f(n)+n+2)$

于是，对于任意$k$次多项式$f(n)$，有$NSPACE(f(n))=NSPACE(n^k)$，则可定义复杂类

$$NPSPACE=\underset{k\geq 0}{\cup}NSPACE(n^K)$$

非确定图灵机判定旅行商问题

    $TSP(D)$问题是一个经典的问题，假设有$n$个城市，分别记为$1,2,\cdots,n$。任意两个城市$i$和$j$之间有距离$d_{ij}$且$d_{ij}=d_{ji}$，问能否找到一个最短的旅行路线，即找到一个$\{1,2,\cdots,n\}$上的置换$\pi$ 使得$\sum_{i=1}^n d_{\pi(i)\pi(i+1)}$尽可能地小，此问题称之为$TSP$问题。也可以定义其判定性问题：

$TSP(D)$：给定非负整数$B$及矩阵$(d_{ij})$，其中$d_{ij}>0$，问是否有一个长度小于等于$B$的旅行线路？

显然，穷举所有可能可以解此问题，但代价是所用时间与$n!$成比例，由于需要存储当前的置换和最佳路线，故所需空间与$n$成比例。

    目前还不清楚$TSP(D)$是否在$P$中，但其必然属于$NP$，因为可以构造一个非确定图灵机$N$在时间$O(n^2)$内判定此问题。图灵机的设计也非常简单，设$x$为$TSP(D)$的一个实例表示，对于输入$x$，$N$继续写一个长度不超过$x$的任意符号序列$y$，这个写入当然是通过转移函数$\Delta$实现的，由于$N$是一个非确定图灵机，转移函数是一个关系而不是映射，所以我们构造的转移函数的转移路径可以任意多，一个路径对应一个$y$串，可以遍历所有的$y$串，虽说是遍历，但这显然也是符合非确定图灵机的定义的，因为$N$只是随机选择一个路径执行后面的操作。

    接着$N$返回指针并检查$y$是否为城市的一个置换的表示，若是一个置换，则检查该置换的旅行代价是否$\leq B$。这两项任务可在时间$O(n^2)$内完成(必要时可用另外一条带)，若该串$y$的确编码了一个代价比$B$小的旅行，则机器接受，否则，拒绝。

    注意，这里需要有一个“猜测”的机器运算，然后检查是否为置换，由这个例子可以看出，若输入$x$是一个$yes$实例，则机器可以猜测一个恰当的置换，并验证得此旅行代价刚好$\leq B$，也许其它的猜测都被拒绝，但无所谓，只要有一个猜测成功即可。反过来，若发现所有计算的猜测都不满足$\leq B$，输入将被拒绝。

确定图灵机模拟非确定图灵机

    由旅行商问题可以看出，非确定图灵机的能力是非常强大的，比确定图灵机的能力强的多，目前我们不知道如何将非确定图灵机多项式代价的转变为一个确定图灵机，但下面定理为我们提供了指数代价的转变方法。

设非确定图灵机$N$在时间$f(n)$内判定语言$L$，则存在一个3-带确定图灵机$M$在时间$O(c^{f(n)})$内判定$L$，其中$c>1$是一个依赖于$N$的常数。

这个定理的证明略，在老师的讲义上有。