图灵机是现在主要在研究的计算模型，也是复杂性理论的基础计算模型，我之前只是有个模糊的了解，从结构上看，它是一个很弱的计算模型，但它能够表达任意的算法，模拟任意的计算模型。这里我详细给出图灵机的基础定义和例子，另外这里给出的定义实际上是确定图灵机的定义。

    首先需要了解图灵机的基础构造，图灵机存在唯一的数据结构：字符串。字符串由字母表$\Sigma$定义，是$\Sigma$中的字符连接而成，一般只考虑$\Sigma=\{0,1\}$时的字符串，同时设$\Sigma^*$为$\Sigma$上所有字符串构成的集合。图灵机有两个最基本的结构单元：控制单元和存储单元。控制单元通常被称为有限控制器，它有有限个状态，存储单元由一条或数条无限带组成，一般都是假设这些带左端固定，右端无限延长，每条带被分成无限个小方格，每格可以存储一个字符。有限控制器和带之间通过指针来联系，如下图所示：

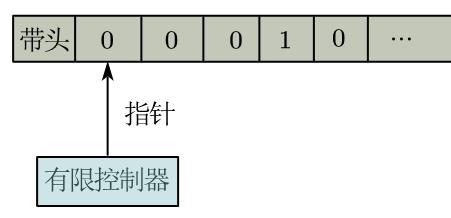
这里的指针是非常重要的一个结构，首先其移动时每次只能移动一个方格，方向或左或右，指针在其指向位置的格子上可以完成读写当前字符和擦除当前字符这些操作。

    图灵机的形式定义比较冗长，图灵机是一个四元组$M=\{K,\Sigma,\delta,s\}$，满足下面六个条件：

1. $K$是一个有限状态集合，$s\in K$是图灵机的初始状态
2. $\Sigma$为$M$的字母表，是一个与$K$无关的有限字符集合。$\Sigma$总含有两个字符，空格$\cup$和带上的带头$\rhd$
3. $h,yes,no$是三个与$M$无关的状态，$h$是停机状态，表示机器进入该状态后停机，$yes$是接受状态，表示机器进入该状态后停机并接受输入，$no$是拒绝状态，表示机器进入该状态后停机并拒绝输入
4. 指针有三个移动方向的符号：$\rightarrow$表示指针要向右移动；$\leftarrow$表示指针要向左移动；$-$表示指针不动
5. $\delta$是转移函数，是一个从$K\times \Sigma$到$(K\cup \{h,yes,no\})\times \Sigma\times \{\rightarrow,\leftarrow,-\}$的映射，即 $$\begin{array}{c} \delta: K \times \Sigma \longrightarrow\left(K \cup\left\{h, yes,no\right\}\right) \times \sum \times\{\rightarrow, \leftarrow,-\} \\ (q, \sigma) \longrightarrow(p, \rho, D)=\delta(q, \sigma) \end{array}$$ 这里函数$\delta$即为$M$的“程序”，对于控制器中当前状态$q$和指针所指字符$\sigma$，其函数值为$(p,\rho,D)$，即此时机器的状态变为$p$，字符$\sigma$改写为$\rho$，然后指针向方向$D$移动一格，其中$D\in \{\rightarrow, \leftarrow,-\}$。很显然，转移之后，原格子里的字符发生了改变，之后指针也移动了一次。特别的，当$\sigma=\rhd$时，即指针处于带头上时，转移函数的作用效果如下(状态为初始状态$s$) $$(s,\rhd) \xrightarrow{\delta} (s,\rhd,\rightarrow)$$ 即，当指针指着$\rhd$时，总是要向右移动，不能向左，且符号$\rhd$不能被改写。
6. 图灵机的运行并不复杂，设$M$的输入字符串为$x$，即$x\in\Sigma^*$，带上的符号串为$\rhd x$，指针初始时指着第一个符号$\rhd$，然后机器根据转移函数$\delta$，不断的改变状态和读写字符，同时移动指针，如此下去，直到进入状态$\{h, yes,no\}$中的其中一个时停机，此时，关于输入$x$，机器$M$的输出记为$M(x)$。当$Μ$进入状态$yes$时，$M(x)=yes$，表示接受$x$；当$Μ$进入状态$no$时，$M(x) =no$，表示拒绝$x$；当$Μ$进入状态$h$时，若$Μ$带上的串为$y$，其中$y$的最后一个符号可能不为$\cup$，$y$亦可能为一串$\cup$，则$M(x) = y$，即输出带上的内容。若$Μ$不停机，则记为$M(x) =\nearrow$，表示关于输入$x$，$Μ$不停机。

    显然转移函数的构造就是图灵机的程序，是它指导着指针来回移动，擦除，读写，得到最后的计算结果。另外图灵机的计算过程经常用瞬时像形式表示，图灵机$M$的瞬时像是一个三元组$(q,w,u)$，其中$q\in K$为当前状态，$w,u\in \Sigma^*$且指针指着$w$的最后一个字符，$u$为指针右边的串，也可能为空串。显然瞬时像表示了一个时刻的当前状态，字符串和指针的位置。

字符串前加空格的图灵机模型

    这里给出一个图灵机的例子，考虑图灵机$M=\{K,\Sigma,\delta,s\}$，其功能很简单，就是在带头$\rhd$与字符串之间加一个空格$\cup$。这里最重要的就是转移函数$\delta$的构造，构造好$\delta$之后，这个图灵机可以对任意字符串完成加空格的操作，先令$K=\{s,q,q_0,q_1\}$，$\Sigma=\{0,1,\cup,\rhd\}$，定义转移函数如下：

$(K,\Sigma)$	$(s,0)$	$(s,1)$	$(s,\cup)$	$(s,\rhd)$	$(q,0)$	$(q,1)$
$\delta (K,\Sigma)$	$(s,0,\rightarrow)$	$(s,1,\rightarrow)$	$(q,\cup,\leftarrow)$	$(s,\rhd,\rightarrow)$	$(q_0,\cup,\rightarrow)$	$(q_1,\cup,\rightarrow)$
$(K,\Sigma)$	$(q,\cup)$	$(q,\rhd)$	$(q_0,0)$	$(q_0,1)$	$(q_0,\cup)$	$(q_1,0)$
$\delta (K,\Sigma)$	$(q,\cup,-)$	$(h,\rhd,\rightarrow)$	$(s,0,\leftarrow)$	$(s,0,\leftarrow)$	$(s,0,\leftarrow)$	$(s,1,\leftarrow)$
$(K,\Sigma)$	$(q_1,1)$	$(q_1,\cup)$	$(q_1,\rhd)$
$\delta (K,\Sigma)$	$(s,1,\leftarrow)$	$(s,1,\leftarrow)$	$(h,\rhd,\rightarrow)$

    显然按照转移函数一步步进行，可以最终达到停机状态并完成计算。这里有一个需要注意的地方，在$\rhd$和字符串之间加空格这个操作，是要占用字符串后面的一个空格的，而且$\delta$要求在状态$s$时，只要碰到空格就往回走，所以输入$x$中不能有空格，否则会出错，比如把$\rhd 010\cup 00$计算为$\rhd \cup 01000$，这就出了问题，可以要求输入$x$中无空格$\cup$来避免这个错误。