前一篇博文分析了一阶逻辑的图论模型中的$\phi$-GRAPHS问题，得到结论是对于任何$\Sigma_G$上的表达式$\phi$，$\phi$-GRAPHS问题是多项式时间可解的。这里非常重要的一点是 “任何$\Sigma_G$上的表达式$\phi$”，也就是说虽然句子$\phi$可以在确定多项式时间内被判断出是满足还是不满足的，但这个句子$\phi$必须是$\Sigma_G$上的表达式，或者说$\Sigma_G$上的一阶逻辑表达式，所以一阶逻辑表达式能完整的表达所有图上的问题吗？实际上这显然是不可能的，一阶逻辑存在局限性。

一个引理

    在讨论一阶逻辑的局限性之前，需要先引入一个引理，具体内容如下：

若句子$\phi$有任意大规模(cardinality)的有限模型，则$\phi$有一个无限模型

这个引理的证明很麻烦，这里不再详细给出。引理想表达的是如果一个$\Sigma_G$对任意大小的图都存在一个模型$\Gamma$，则$\Sigma_G$对一个无限图必然存在一个模型$\Gamma’$，这里图的大小意味着图的顶点个数。

一阶逻辑无法表达REACHABILITY问题

    之前我们用一阶逻辑表达了图的性质：出度为1、对称性、传递性等；并且证明了可由一个句子$\phi$表达的图的性质是容易验证的，即$\phi$-GRAPHS问题有多项式时间算法。那么，是否所有的多项式可验证的图的性质都可用一阶逻辑表达？答案是否定的。实际上利用上面的引理可以证明REACHABILITY问题不能用一阶逻辑表达式表示。

没有(有两个约束变元$x$和$y$的)一阶逻辑表达式$\phi$使得$\phi$-GRAPHS问题与REACHABILITY问题等价

    为了证明这个定理，首先假设某个句子$\phi$的$\phi$-GRAPHS问题等价于REACHABILITY问题，则可定义如下三个一阶逻辑表达式：

$$\psi_0=\forall x\forall y\phi \qquad \psi_1=\forall x \exists y G(x, y) \wedge \forall x \forall y \forall z(G(x, y) \wedge G(x, z) \Rightarrow (y=z))$$ $$\psi_2=\forall x \exists y G(y, x) \wedge \forall x \forall y \forall z(G(y, x) \wedge G(z, x) \Rightarrow (y=z))$$

其中$\psi_0$表示图中的任意两个点都存在通路，即为强连通的，$\psi_1$说明每个顶点的出度为1，$\psi_2$说明每个顶点的入度为1，设$\psi=\psi_0\land\psi_1\land\psi_2$，易得$\psi$必为一个圈，如下图所示(6个顶点的圈)。

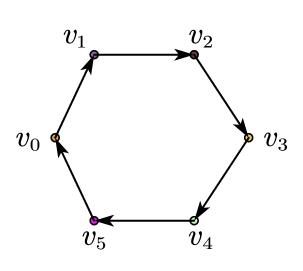
    显然只要给定了顶点个数，这种圈是必然存在的，且不止一个，故句子$\psi$有任意大的有限模型，由前面引理可知$\psi$必然存在一个无限模型$G_\infty$，也就是对应的图有无穷多个顶点。接下来主要考虑$G_\infty$，$G_\infty$的顶点个数必然是可数的，不妨设这个圈对应的顶点序列为$v_0,v_1,v_2,\cdots$，其中$(v_i,v_{i+1})$为边，且所有的顶点出度和入度均为1，故$v_0$的入度为1，于是存在某个顶点$v_j$，$v_j$必然处于序列$v_0,v_1,v_2,\cdots$中的某个位置且$(v_j,v_0)$为一条边，则此时$G_\infty$对应的图必然有$j+1$个点，显然为有限图，这与$G_\infty$是无限图矛盾，故原假设不成立，即与REACHABILITY问题等价的$\phi$-GRAPHS问题是不存在的，即一阶逻辑表达式表达不了REACHABILITY问题。

    直观上说，一阶逻辑中的量词仅仅关注于一个元素的性质，比如$\forall x$，它就仅仅关注于$x$，再加上关系的话，它也就仅仅关注于$x$的一步关系，比如$\forall x\exists y G(x,y)$，表示$(x,y)$有一条边，这仅仅是一步关系，但REACHABILITY问题关注的是$x$与$y$之间有没有通路，这个通路可能不是一步关系，可能是很多步的关系，比如经过很多边之后才形成通路。由此可见，REACHABILITY问题是一阶逻辑不可表达的。但该结果是很有趣的，主要原因是这是一个非平凡的不可能结论，该结论恰是复杂性理论中所要研究的结果类型。而且这种不可能结果促使我们对一阶逻辑进行了推广研究，比如在关系之间加入量词，也就是二阶逻辑。