一阶逻辑在语义上将句子和其应用的数学对象视为等同，具有强大综合性的原始证明系统，为我们提供用于详细表达数学命题的语法。与Boolean逻辑相比，它能表达更广泛的数学思想和事实；这些表达涉及了数学各领域的常数、函数和关系。当然，每个表达式仅涉及这些中的一个小部分。因此，利用一阶逻辑，我们可以统一地研究定义域上的所有推理。

词汇表定义

    词汇表$\Sigma=(V,\Phi,\Pi,r)$定义如下

1. $V$为固定的可数变量集合$V={x,y,z \cdots}$，其中所有变量取值于由特定表达式所讨论事物全体组成的定义域，不同模型的定义域有所不同。
2. $\Phi$为函数符号集合，$\Pi$为关系符号集合，$\Phi \cap \Pi =\emptyset$
3. $r$为一个计数函数，将$\Phi \cup \Pi $映到非负整数，即说明每个函数和关系符号取多少个变量。
4. 如果$f\in \Phi$且$r(f)=k$，则称$f$是一个$k$元函数，如果$R\in \Pi$且$r(R)=k$，则称$R$是一个$k$元关系
5. 常数为0元函数，另外这里假设$\Pi$总含有二元相等关系。

一阶逻辑表达式

    有了词汇表的定义，就可以定义定义一些表达式，和Boolean逻辑一样，这些表达式可以用逻辑符号连接，如$\neg,\land ,\lor ,\forall$等等。但一阶逻辑表达式并不是直接就可以定义的，首先要给出单项式(Term)和表达式(Atomic)的定义。

单项式(Term)的归纳定义：

1. $V$中的任何变量都是Term
2. 若$f\in \Phi$且$r(f)=k$，$t_1,\cdots ,t_k$为Term，则$f(t_1,\cdots ,t_k)$也为Term
3. 常数也为Term

表达式(Atomic)的定义：若$R\in \Pi$且$r(R)=k$，$t_1,\cdots ,t_k$为Term，则$R(t_1,\cdots ,t_k)$为表达式(Atomic)。即Atomic是Term加上关系。

一阶逻辑表达式的归纳定义：

1. 所有的Atomic都是一阶逻辑表达式
2. 若$\phi$与$\psi$均为Atomic，则$\neg \phi,\neg \psi,\phi \lor\psi,\phi \land \psi$也是一阶逻辑表达式
3. 若$\phi$为Atomic，$x$为变量，则$\forall x\phi$也是一阶逻辑表达式，其中$\forall$是全称量词，对应的$\exists$是存在量词，$\phi$称为$x$的辖域，$\phi$中的变元$x$称为约束变元，其余变元称为自由变元。($\exists x\phi$等价于$\neg(\forall x\neg \phi)$)

一阶逻辑表达式的赋值

    一阶逻辑的表达式定义已经给出，接下来要考虑一阶逻辑表达式的赋值，一阶逻辑的真值是由各部分真值取值来决定的，故需要一个确切的模型，也就是一个将一阶逻辑赋予实际意义的“环境”，这个模型也是一个更复杂的数学对象。对于词汇表$\Sigma=(V,\Phi,\Pi,r)$，适合$\Sigma$的模型是一个二元关系$M=(U,\mu)$，满足下列性质:

1. $U$是一个集合，称为二元关系$M=(U,\mu)$的定义域
2. $\mu$是一个函数，$\mu$给$V\cup \Psi\cup \Pi$中的每个变量，函数符号和关系符号分配一个$U$中的对象，对于每个变量$x$，$\mu$的赋值为$x^M \in U$，对于每个$k$元函数符号$f\in \Phi$，$\mu$的赋值为函数$f^M:U^k\rightarrow U$，若$c\in\Phi$是常数，则$\mu$的赋值为$c^M\in U$，对每个$k$元关系$R\in \Pi$，$\mu$的赋值为$R^M\subseteq U^k$。对于相等关系“=”，$\mu$的赋值为$=^M$，即${(\mu,\mu):\mu \in U}$

    定义了模型之后，考虑一阶逻辑表达式的赋值，也就是在一个模型下一阶逻辑表达式满足不满足。给定一个$M$，要考虑一阶逻辑表达式满不满足，要先定义出单项式在$\mu$下的像，若单项式$t$为变量或常数，则$t$在$\mu$下的像为$t^M$，若$t=f(x_1,\cdots,x_k)$，则定义$t$在$\mu$下的像为$t^M=f^M(x_1^M,\cdots,x_k^M)$，接下来讨论一阶逻辑表达式$\phi$在模型$M$下如何被满足：

1. 若$\phi$是一个Atomic，即$\phi=R(t_1,\cdots,t_k)$，则若有$(t_1^M,\cdots,t_k^M)\in R^M$，则称$M$满足$\phi$，记为$M|=\phi$
2. 若$\phi=\neg \psi$，则若有$M|\neq \psi$，则称$M|=\phi$
3. 若$\phi=\psi_1\lor\psi_2$，当$M|=\psi_1$或$M|=\psi_2$时，则称$M|=\phi$，若$\phi=\psi_1\land\psi_2$，当$M|=\psi_1$且$M|=\psi_2$时，则称$M|=\phi$
4. 若$\phi=\forall x \psi$，考虑$u\in U$，设$M_{x=u}$是一个除了$x^{M_{x=u}}=u$之外均等同于$M$的模型，若$\forall u\in U$，均有$M_{x=u}|=\psi$，则称$M|=\phi$

    $\forall x\phi$是一个一阶逻辑表达式，若$\phi$中没有自由变元，则$\forall x\phi$叫做一个句子，在一个确定的模型下，一个句子满不满足是完全确定的，所以一个模型会存在许多被满足的句子，一个句子也肯定会对应有满足此句子的许多模型，即一个句子刻画了模型的一个性质。所以句子和模型之间存在一个对偶的关系。

一阶逻辑表达式的一个例子

    这个例子是图的例子，首先定义词汇表$\Sigma_G=(V_G,\Phi_G,\Pi_G,r_G)$，其中$V_G=\{x,y,z\cdots\}$为变量集合，$\Phi_G=\emptyset$，$\Pi_G=\{=,G\}$，即除了“=”之外还有一个二元关系$G$，这样就可以写出这个词汇表的一些一阶逻辑表达式如$G(x,x)$，$\exists x(\forall yG(y,x))$，$\forall x(\forall y(G(x, y) \Rightarrow G(y, x)))$，$\forall x(\forall y(\exists z(G(x, z) \wedge G(z, y)) \Rightarrow G(x, y)))$等等，但此时$x,y,z,G$还没有具体的意义，只有把$\Sigma_G$对应的模型$\Gamma=(U,\mu)$确定下来后$x,y,z,G$才有确定的意义。

    这里的$\Gamma=(U,\mu)$实际上与一个确定的图$H$相关，$U$就是这个图$H$的顶点集合，$\mu$是一个映射，将变量集合$V_G$一一映射为图$H$的顶点集合$U$，将二元关系$G$映射为图$H$的边集合$T$($T$显然是集合$U$上的一个二元关系)，显然这是满足上面给出的模型的定义的，这里不妨设图$H$如下图所示(这里均考虑有限图)。

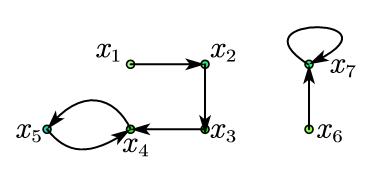
显然$U=\{x_1,\cdots,x_7\}$，则易知$V_G$中有7个变量，至此，$\Sigma_G$的模型$\Gamma$就完全定义了。

    接下来要考虑一阶逻辑表达式是否满足，比如$G(x,x)$，根据上面给出的一阶逻辑表达式满足或不满足的判断方法，$G(x,x)$是一个Atomic，$x$在$\mu$下的像为$x_1$，且根据图$H$，$(x_1,x_1)\notin T$即$(x_1,x_1)\notin G^\Gamma$，则显然$\Gamma$不满足$G(x,x)$，即$\Gamma |\neq G(x,x)$，再如$\exists x(\forall yG(y,x))$，当$y=x$时，由于$\Gamma |\neq G(x,x)$，则显然$\Gamma |\neq \exists x(\forall yG(y,x))$。

    设$\phi_1=(\forall x \exists y G(x, y)) \wedge \forall x \forall y \forall z(G(x, y) \wedge G(x, z) \Rightarrow y=z)$，对于模型$\Gamma$来说，可以一一验证，$\Gamma$必然满足$\forall x \exists y G(x, y)$且满足$\forall x \forall y \forall z(G(x, y) \wedge G(x, z) \Rightarrow y=z)$，则有$\Gamma |= \phi_1$，实际上这里的句子$\phi_1$就是说明了图的一个性质，即一个模型$\Gamma$满足$\phi_1$当且仅当此模型$\Gamma$对应的图的所有顶点的出度为1，显然上面的图$H$是满足这一点的。

    设$\phi_2=\forall x(\forall y(G(x, y) \Rightarrow G(y, x)))$可以发现$\Gamma$不满足$\phi_2$，因为$\Gamma$对应的图$H$是“不对称”的，所以某个模型$\Gamma_1$满足$\phi_2$就等价于模型$\Gamma_1$对应的图是对称图，同样的，句子$\phi_3=\forall x(\forall y(\forall z(G(x, z) \wedge G(z, y)) \Rightarrow G(x, y)))$也描述了一个性质，某个模型$\Gamma_2$满足$\phi_3$就等价于模型$\Gamma_2$对应的图是传递图。

    到此，这个与图相关的例子就结束了，但实际上我们发现这里的每个句子都描述了图的一个性质，当然，图的任何性质也对应于一个计算问题：给定一个图，问该图是否具有这个性质？我们称此问题为$\phi$-GRAPHS问题，严格说就是：

设$\phi$是一个$\Sigma_G$上的一阶逻辑表达式，给定一个关于$\phi$的模型$\Gamma$，是否有$\Gamma|=\phi$？
这是一个判定问题，此问题的分析由于博文篇幅原因，见下一篇博文。