Boolean电路与Boolean表达式的等价在NP问题的相互归约里也会用到，这里讨论一下它们的基本定义和性质。

Boolean电路

    一个Boolean电路是一个图$C=(V,E)$，其中顶点集合$V=\{1,2,\cdots , n\}$，每个顶点都被称为门，其中顶点$n$为电路的输出门。图$C$有下列特点：

1. 图$C$中没有圈，故可以设此图的边为$(i,j)$，均满足$i< j$
2. 所有顶点的入度可能为0，1，2三种
3. 每个顶点(或门)$i \in V$都是集合$S$中的一个元素，$S:=\{0,1,\neg, \land ,\lor, x_1,x_2,\cdots ,x_t \}$，即每个顶点都从集合$S$中选择，其中$x_1,x_2,\cdots ,x_t$是Boolean变量。若$i\in \{0,1, x_1,x_2,\cdots ,x_t \}$，则$i$的入度为0，即没有进入$i$的边，若$i=\neg$，则$i$的入度为1，若$i\in \{ \land ,\lor\}$，则$i$的入度为2。

    令$X(C)$为出现在$C$中的所有Boolean变量的集合，即$X(C)=\{ x_1,x_2,\cdots ,x_t \}$，称一个赋值$T$是适合$C$的，如果$T$对于$X(C)$中的所有变量都有定义。对于每个合适的赋值$T$，电路$C$都描述了一个真值，这个真值的计算过程也并不复杂，首先每一个门$i$都有一个真值$Q(i)$，若门$i$是1，则$Q(i)=1$，若门$i$是0，则$Q(i)=0$，若门$i$是$x_m \in \{ x_1,x_2,\cdots ,x_t \}$，则$Q(i)=T(x_m)$，若门$i$是$\neg$，则必然存在唯一的门$j$满足$j< i$ ，使得$(j,i)\in E$，则$Q(i)=\neg T(j)$，若门$i$是$\lor$，则必有两条边$(j,i)$和$(j’,i)$进入$i$，则有$Q(i)=T(j)\lor T(j’)$，若门$i$是$\land$，则必有两条边$(j,i)$和$(j’,i)$进入$i$，则有$Q(i)=T(j)\land T(j’)$，这样，层层归纳，一定可以得到最后一个门的真值$Q(n)$，而$Q(n)$就是这个电路$C$在赋值$T$下得到的真值，也记做$T(C)$。

    相应于Boolean电路，也有一个计算问题，称为CIRCUITSAT，即给定一个电路$C$，是否有适合$C$的赋值$T$满足$T(C)=1$。由定义可以看出Boolean电路与Boolean表达式是一致的，可以互相构造，所以显然CIRCUITSAT与SAT是计算等价的，即可以相互归约，若一个电路$C$没有变量门，则对应问题为CIRCUIT VALUE，只需按顺序计算所有门即可，这显然是多项式时间可以求解的。

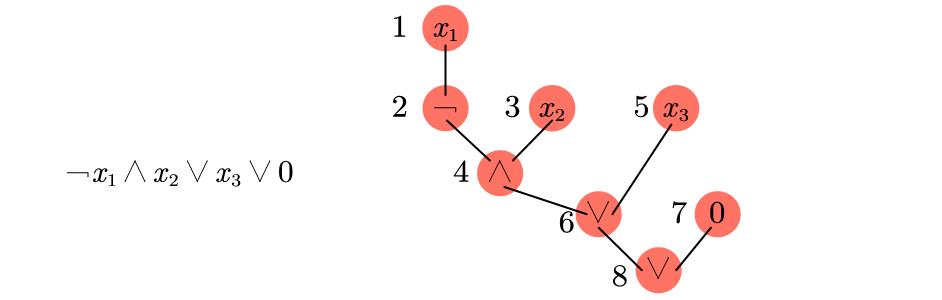
Boolean电路与Boolean表达式转化的例子

    这里给出一些Boolean表达式转化为Boolean电路的例子，如下两图所示，其中画红圈的表示门，旁边的数字表示顶点顺序。

赏

谢谢你请我喝冰露

支付宝

微信