问题简介

    首先给出二分图的定义，二分图是一个三元组$B=(U,V,E)$，其中$U=\{u_1 \cdots u_n\}$，是一个点集，$V=\{v_1 \cdots v_n\}$，也是一个点集，$E$是一个边集合，满足$E\subseteq U\times V$。二分图的一个匹配是指一个$n$条边的集合$M$，满足$M\subseteq E$，且对任意两条边$(u,v),(u',v')\in M$，一定满足$u\neq u’,v\neq v’$，即$M$中没有边是邻接的，或者说没有边是共用顶点的。如下图所示，其中的红色部分就是一个二分图的匹配。

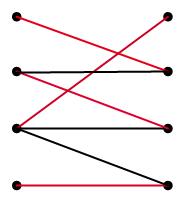
现在需要解决的问题就是一个二分图是否存在一个匹配？这是一个判定问题，只需要回答有或没有即可。

算法思想与算法分析

    这里用到了归约的思想，也就是把二分图的匹配问题归约到MAXFLOW问题，然后利用MAXFLOW问题的算法判定一个二分图是否有匹配。首先对二分图$B=(U,V,E)$构造一个网络$N=(V,E’,s,t,c)$，其中$V=U\cup V $，$E'=\{(s,u):u\in U\}\cup \{(v,t):v\in V\}\cup E$，各个边上的容量$c$均为1。下面的两个图是一个二分图和由此二分图构造的网络，显然构造非常简单。

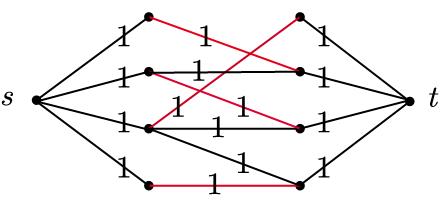
    显然二分图$B=(U,V,E)$存在匹配等价于网络$N=(V,E’,s,t,c)$的最大流为$n$，这个也是非常好理解的，因为最终连接$t$的就是$n$条边，每条边的容量都是1，而从$s$出发的边刚好也是$n$个，每条边的容量也是1，故匹配存在就等价于$U$和$V$之间存在一个一一对应，而一一对应存在也等价存在一个为$n$的流量，显然$n$必为最大流，故二分图$B=(U,V,E)$存在匹配等价于网络$N=(V,E’,s,t,c)$的最大流为$n$。

    故解决二分图的匹配问题只要先构造一个网络，然后调用一次MAXFLOW问题的算法即可，若最大流为$n$，则存在匹配，否则不存在匹配。由于构造网络的边的容量均为1，由之前博文MAXFLOW问题算法的复杂度分析可知，解决二分图的匹配问题的算法复杂度为$O(n^3)$。

赏

谢谢你请我喝冰露

支付宝

微信