问题简介

    图论中的MAXFLOW问题，也叫作极大流量问题，这个问题是REACHABILITY问题的一个推广。一个网络$N=(V,E,s,t,c)$是一个带有两个特定顶点$s$和$t$的图$(V,E)$，其中称$s$为源，$t$为接收器。并且没有进入源$s$的边，也没有离开接收器$t$的边，对每条边$(i,j)$，给定一个称为容量的正整数$c(i,j)$。
    $N$中的一个流量$f$是对每条边$(i,j)$的一个非负整数赋值$f(i,j)\leq c(i,j)$，满足除了$s$和$t$外，每个顶点的进入边的$f$值的和等于其离开边的$f$值的和。一个流量$f$的值则是离开$s$，到达$t$的边的流量的和。极大流量问题就是给定一个网络$N$，找到一个最大可能值的流量。
    这个问题本科图论中也讲过，但方法和复杂性课上有些区别，是利用寻找增广链来寻找最大流，但当时没有估计算法的复杂度，这里主要写复杂性课上讲的构造导出网络的方法。

算法思想

    算法的思想并不复杂，首先已知网络$N=(V,E,s,t,c)$中已经有了一个流$f$，这个流是初始的流，接着要对这个流构造导出网络，构造导出网络的方法也很简单，具体流程如下

1. 原网络$N=(V,E,s,t,c)$，依据流$f$构造的导出网络记为$N(f)=(V,E’,s,t,c’)$
2. 满足$f(i,j)=c(i,j)$的边$(i,j)$要进行反向，即原来的$(i,j)$变为$(j,i)$，且容量不变，$c’(j,i)=c(i,j)$
3. 满足$f(i,j)=0$的边$(i,j)$不做任何变化，方向不改变，容量不变，$c’(i,j)=c(i,j)$
4. 满足$f(i,j)< c(i,j)$的边，首先要对边的容量进行变化，，原来的$c(i,j)$变为$c’(i,j)=c(i,j)-f(i,j)$，然后在边$(i,j)$的基础上新增一条边$(j,i)$，其容量为$c’(j,i)=f(i,j)$

    导出网络的构造是非常简单的，直接看流程并不清晰，可以结合例子看更加清楚，首先给出一个网络$N=(V,E,s,t,c)$如下

接着给出此网络上的一个流如下 接着利用前面的流程，得到导出网络$N(f)=(V,E',s,t,c')$如下

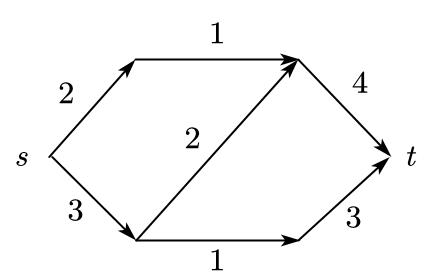
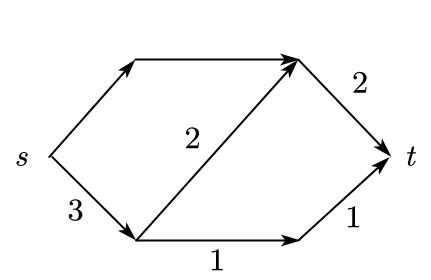
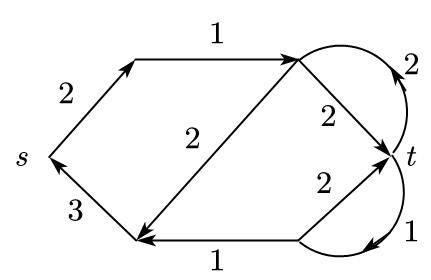
    接着分析导出网络的作用，首先对于$f(i,j)=c(i,j)$的边，这些边上的流量不可能再增加了，只能减少，减少可以理解为反向的流量，所以在导出网络里将满足$f(i,j)=c(i,j)$的边直接反向且容量不变；满足$f(i,j)=0$的边$(i,j)$相当于根本没有用到，这种边还可以承受正向的流量，所以这些边不做任何变化；满足$f(i,j)< c(i,j)$的边，首先边的容量没满，它还可以承受$c(i,j)-f(i,j)$的流量，所以要留一个正向容量$c’(i,j)=c(i,j)-f(i,j)$的边，由于已经有了$f(i,j)$的流量，这些流量由于是固定的，只能减少，不能增加，因为增加相当于是对正向容量为$c’(i,j)=c(i,j)-f(i,j)$的边增加的，所以这些容量只能减少，故要在边$(i,j)$的基础上新增一条边$(j,i)$，其容量为$c’(j,i)=f(i,j)$，意味着如果这条边上有流量，就是原来的流量减少。

    所以如果导出网络存在$s$到$t$的通路，则原来的流$f$必然不是最大流，还有增加的余地，可增加的量就是这条通路上的最小容量，故这就将MAXFLOW问题归约到了可达性问题上，可达性问题是存在$O(n^2)$的算法的，故解决MAXFLOW问题只需要调用可达性问题的算法即可。

算法流程与复杂度分析

    解决MAXFLOW问题的算法流程如下

1. 设初始流量$f$为零流，即处处的流量均为零，执行下一步
2. 对流量$f$，构造导出网络$N(f)$，并对$N(f)$应用可达性问题的求解算法，若$N(f)$中存在$s$到$t$的通路，则沿此通路找到最小的容量$c’$，并将$c’$加到该通路上所有边的$f$值上，得到更大的流$f$
3. 重复第二步，直到找不到$s$到$t$的通路，输出流$f$

    显然此算法可以完成最大流的计算，接着分析此算法的复杂度。首先算法每次重复地对导出网络$N(f)$找到一条通路，并增加该通路上的流量，每执行一次所用的时间和可达性问题一样，为$O(n^2)$。事实上，每次执行可达性的算法之后，流量至少增加1(我们的分析都是假设现在的流$f$还不是最大流)，若$C$为网络中边的最大容量，则最大流量不会超过$nC$(因为终点$t$最多只能与$n-1$个点相连)，故可达性问题的算法至多需要重复$nC$次，因此解决MAXFLOW问题的总时间为$O(Cn^3)$。

    注意，虽然看起来是一个多项式，但由于$C$的存在，只能是一个伪多项式，因为$C$可能是指数的，比如下面的这个网络，如果按照上面的算法从零流开始，如果每次找通路的运气不好，总是找不到$(s,b,t)$和$(s,a,t)$这样的通路，它是的确需要调用$2C$次可达性问题算法的(具体分析略了，这个很简单)，所以需要新的分析复杂度的方式。

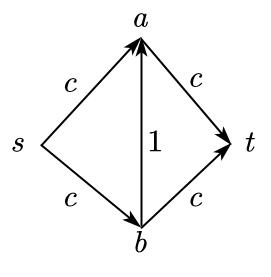
    为克服这个缺陷，我们先用可达性问题算法宽度优先的方式找到最短通路，然后沿着最短通路增加流量，一条通路上有最小容量的边称之为瓶颈，故每次增加流量相当于克服一个瓶颈。整个网络至多有$n^2$条边，故瓶颈至多$n^2$个，且每次重复必然克服一个瓶颈，由于每条通路至多有$n$条边，在每一条边上都有可能出现瓶颈，故最多只重复$n^2 \cdot n=n^3$次可达性问题算法即可克服所有瓶颈，找到最大流，则此时复杂度为$O(n^5)$。于是可以在时间$O(n^5)$内解决MAXFLOW问题。

    接着分析算法的空间使用情况，算法的每次重复需要空间很小，类似于可达性问题，为$O(log^2n)$，但需要额外的$O(n^2)$空间存储当前的流，因为最多是$n^2$条边，故总的空间复杂度还是$O(n^2)$的。

    所以MAXFLOW问题是多项式时间可解的。